質量を持った物体が動いているとき、その物体は運動エネルギーを持っているということはよく知られています。エネルギー量は質量と速度という２つのパラメータで表現することができます。エネルギーを一般的に定義することは難しいことですが、その量は簡単に測ることができます。ビリヤードの玉のような質量Mの玉Aが速度Vで静止している同じ質量の玉Bの中心に衝突するとします。
このとき衝突する前の玉AはMVに比例する運動のエネルギーを持っていると表現することにしましょう。衝突する前の玉Bは速度ゼロですから、運動のエネルギーもゼロであると見なすことにしましょう。玉Aが玉Bに衝突すると、玉Aが静止し、玉Bが速度Vで走り出すとします。
このとき、初めに玉Aにあった運動のエネルギーが玉Bに移ったと考えることができます。このようにして、エネルギーは移動することができます。このとき全体の運動のエネルギーは、衝突前と衝突後で同じになっています。これはエネルギー保存の法則とよばれているものの最も基本的で重要な例です。このような方法を応用して、棒で壁をついたときに必要なエネルギーはどれだけか測ることは難しいですが、同じ力でボールをつくことによって、そのエネルギー量を知ることができます。
このようにして、加えられたエネルギー量が直接知られていなくても、エネルギーが加えられた物体の速度を測ることによって、そのエネルギー量を知ることができます。複雑な動作に要するエネルギーを簡単な形に換算することができます。
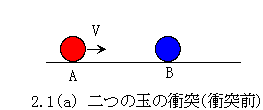
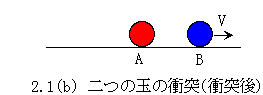
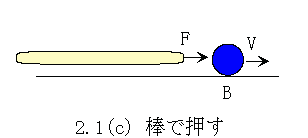
ところで、特に意識せずに速度という量を用いてきましたが、この量は意外と簡単な物理量ではありません。一般的な物理学の知識では、速度という量は相対的な量であると考えられています。それならば、その関数であるエネルギーも相対量ということになります。このように考えるとすぐに困難な問題に直面することになります。速度Vで走っている列車の中から駅を見れば、駅（宇宙？）は反対方向にVの速度で動いていることになります。そこには駅（宇宙？）の質量と速度Vからなる莫大な運動のエネルギーがなければならないことになります。このエネルギーを取り出すことはできるのでしょうか。ここには現実は無く、物理学でしばしば陥る数理表現上の非現実の世界が存在しているように見えます。現象を数理的に表現するという物理学の役割が正しく機能していないと考えられます。それでは物理学では、動いているのは列車であって、駅ではないと表現する方法は存在するのでしょうか。どうすれば、動いているのは列車であって、駅ではないと確かめられるのでしょうか。このことを確かめるのはそれほど難しくありません。列車の速度を減速することで列車と駅の相対速度をゼロにし、その際、放出されるエネルギー量を測ればよいのです。この量は列車を止める前の速度Vと列車の質量に比例する量であることが確かめられることになります。このことから、動いていたのは列車であって、駅ではないと考えることができるでしょう。しかし、列車と相対速度ゼロで運動していた座標系から観測すれば、動いていたのは駅であって、静止していたのは列車であるということも事実には違いありません。本当に動いていたのは、どちらなのでしょうか。物理学を基礎からよく理解しようと努力したことがある人は、われわれが、今、問題にしていることがニュートン以来の空間に関する物理学の最も古い未解決の問題であることに気付いていることでしょう。ニュートンの絶対空間は否定され、物体の速度や運動は相対的であるという考えが一般的な物理学の認識となっています。しかしながら、このような考えが「動いているのが列車であるということを確かめる実験」に矛盾しているということにすぐに気付くことでしょう。相対ではない速度の概念が存在していなければ、現象を数理的に表現できないことになってしまいます。
われわれは、空間や速度という概念について考え直してみる必要があるようです。次には、絶対的な速度の表現を発見することにしましょう。
redsky@graveng.jp
2.2 絶対的な速度
サブメニューに戻る
ホームページに戻る